Recursive, Tree, Graph(DFS, BFS 기초)
- -
1. 피보나치 재귀(메모이제이션)
피보나치를 구현하는 것을 여러 방법으로 풀이해보도록 하겠다.
성능 순으로는 3 -> 2 -> 1 순서로 좋다.
1. 배열을 구현하지 않고 재귀함수를 이용하여 풀이하는 방법
import java.util.Scanner;
public class Main {
public int DFS(int n) {
if(n==1 || n==2) return 1;
else
return DFS(n-2)+DFS(n-1); // 배열 값을 리턴한다.
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i=1; i<=n; i++)
System.out.print(T.DFS(i)+" ");
}
}
2. 재귀 함수를 이용하여 값을 배열에 저장하는 방법
import java.util.Scanner;
public class Main {
static int[] fibo;
public int DFS(int n) {
if(n==1 || n==2) return fibo[n] = 1;
else
return fibo[n] = DFS(n-2)+DFS(n-1); // 배열 값을 리턴한다.
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
fibo = new int[n+1]; // 1번 인덱스부터 필요하므로.
T.DFS(n);
for(int i=1; i<=n; i++)
System.out.print(fibo[i] + " ");
}
}
3. 메모리제이션 방법
배열을 기록하고, 이를 활용하는 방법을 말한다.
import java.util.Scanner;
public class Main {
static int[] fibo;
public int DFS(int n) {
// 이미 값이 있다면 그 값을 그대로 반환한다.
if(fibo[n] > 0 )
return fibo[n];
if(n==1 || n==2) return fibo[n] = 1;
else
return fibo[n] = DFS(n-2)+DFS(n-1); // 배열 값을 리턴한다.
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
fibo = new int[n+1]; // 1번 인덱스부터 필요하므로.
T.DFS(n);
for(int i=1; i<=n; i++)
System.out.print(fibo[i] + " ");
}
}
정리 : 재귀보다는 for문을 이용하는 것이 더 성능이 좋다.
재귀는 스택프레임을 계속 사용하므로 메모리에 이게 쌓이기 때문에 성능적으로 효율적이지 않다.
2. 이진트리순회(DFS : Depth-First Search(깊이우선탐색))

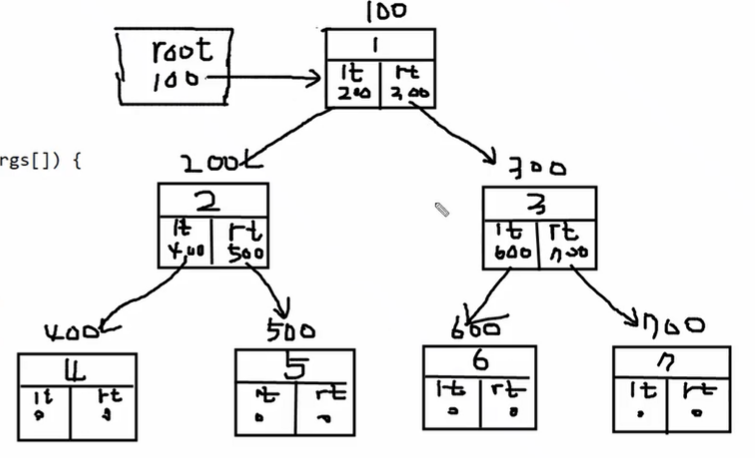
<코드>
import java.util.Scanner;
class Node {
int data; // 실제 값
Node lt, rt; // Node 클래스 객체의 주소를 저장하는 변수.
public Node(int val)
{
data = val;
lt=rt=null; // 처음 생성되면 null값을 가진다.
}
}
public class Main {
Node root; // 객체의 주소를 저장하는 변수.
public void DFS(Node root)
{
//이때 매개변수의 root는 100번지를 의미한다.
if(root==null) return;
else {
// 루트 노드에서는 Left, Right로 두 번 뻗어야 함.
// 전위순회 시 출력 위치
System.out.print(root.data+" ");
DFS(root.lt);
// 중위순회 시 출력 위치
// System.out.print(root.data+" ");
DFS(root.rt);
// 후위순회 시 출력 위치
// System.out.print(root.data+" ");
}
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
tree.root.rt.lt = new Node(6);
tree.root.rt.rt = new Node(7);
tree.DFS(tree.root);
}
}
위와 같은 코드가 있다고 할 때,
tree.root = new Node(1);3. 부분집합 구하기(DFS)
▣ 입력설명
첫 번째 줄에 자연수 N(1<=N<=10)이 주어집니다.
▣ 출력설명
첫 번째 줄부터 각 줄에 하나씩 부분집합을 아래와 출력예제와 같은 순서로 출력한다.
단 공집합은 출력하지 않습니다.
▣ 입력예제 1
3
▣ 출력예제 1
1 2 3
1 2
1 3
1
2 3
2
3
<코드>
import java.util.Scanner;
public class Main {
static int n;
static int[] ch;
public void DFS(int L)
{
if(L == n+1) // 마지막 지점까지 도달했을 때
{
String tmp="";
for(int i=1; i<=n; i++)
{
if (ch[i] == 1)
tmp+=(i+" ");
}
if(tmp.length() > 0) // 0이면 공집합
System.out.println(tmp);
}
else // 계속해서 부분집합을 구해야 할 때
{
ch[L]=1;
DFS(L+1); // 왼쪽으로 뻗는다. (사용O), 부분 종료라고 표시하는 부분
ch[L]=0;
DFS(L+1); // 오른쪽으로 뻗는다. (사용X), 완전 종료라고 표시하는 부분
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
ch=new int[n+1]; // 인덱스 번호 = 숫자를 가르키기 위해
// n이 아닌 n+1로 배열을 생성한다.
T.DFS(1);
}
}
이 코드를 이해하기 위해, 왼쪽 영역의 스택 프레임을 재귀함수를 따라가며 그려보면 아래와 같다.

4. 이진트리 레벨탐색(BFS : Breadth-First-Search(너비우선탐색))

<코드>
import java.util.LinkedList;
import java.util.Queue;
class Node {
int data;
Node lt, rt;
public Node(int val) {
data = val;
lt=rt=null;
}
}
public class Main {
Node root;
public void BFS(Node root)
{
Queue<Node> Q = new LinkedList<>();
Q.offer(root);
int L=0;
while(!Q.isEmpty()) // 비어있지 않다면...
{
int len = Q.size();
// 노드 상태를 확인해보고 싶을 때 확인하는 코드
System.out.print(L+" : ");
for(int i=0; i<len; i++)
{
Node cur = Q.poll();
System.out.print(cur.data+" ");
if(cur.lt != null)
Q.offer(cur.lt);
if (cur.rt != null)
Q.offer(cur.rt);
}
L++;
System.out.println();
}
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
tree.root.rt.lt = new Node(6);
tree.root.rt.rt = new Node(7);
tree.BFS(tree.root);
}
}
5. 송아지 찾기 1(BFS : 상태트리탐색)
현수는 송아지를 잃어버렸다. 다행히 송아지에는 위치추적기가 달려 있다.
현수의 위치와 송아지의 위치가 수직선상의 좌표 점으로 주어지면 현수는 현재 위치에서 송아지의 위치까지 다음과 같은 방법으로 이동한다.
송아지는 움직이지 않고 제자리에 있다.
현수는 스카이 콩콩을 타고 가는데 한 번의 점프로 앞으로 1, 뒤로 1, 앞으로 5를 이동할 수 있다.
최소 몇 번의 점프로 현수가 송아지의 위치까지 갈 수 있는지 구하는 프로그램을 작성하세요.
입력
첫 번째 줄에 현수의 위치 S와 송아지의 위치 E가 주어진다. 직선의 좌표 점은 1부터 10,000까지이다.
출력
점프의 최소횟수를 구한다. 답은 1이상이며 반드시 존재합니다.
예시 입력 1
5 14
예시 출력 1
3<코드> -> BFS를 이용한 탐색방법
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
int[] dis = {1, -1, 5};
int[] ch; // 한번 방문한 Queue에는 방문하지 않음을 확인하기 위한 check 배열
Queue<Integer> Q = new LinkedList<>();
public int BFS(int s, int e)
{
ch = new int[10001]; // 1부터 10000까지 이므로
ch[s]=1; // 출발 지점.
Q.offer(s);
int L=0; // 레벨 값
while(!Q.isEmpty()) // 비어있지 않다면...
{
int len = Q.size();
//System.out.print(L+" : ");
for(int i=0; i<len; i++)
{
int x = Q.poll();
//송아지 위치를 찾을 때 여기에 둬도 된다.
// if(x==e)
// return L;
for(int j=0; j<3; j++)
{
int nx = x + dis[j];
if(nx==e)
return L+1; // 자식노드이므로
if(nx >= 1 && nx <= 10000 && ch[nx]==0)
{
ch[nx]=1;
Q.offer(nx);
}
}
}
L++;
}
return 0;
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
int s = sc.nextInt();
int e = sc.nextInt();
System.out.println(T.BFS(s, e));
}
}
6. Tree 말단 노드까지의 가장 짧은 경로
문제는 아래와 같다.

(1) DFS 풀이법
<코드>
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
class Node {
int data;
Node lt, rt;
public Node(int val)
{
data = val;
lt=rt=null;
}
}
public class Main {
Node root;
public int DFS(int L, Node root)
{
if(root.lt == null && root.rt == null)
return L;
else
{
return Math.min(DFS(L+1, root.lt), DFS(L+1, root.rt));
}
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
// 0단계에 100번지를 넘긴다.
System.out.println(tree.DFS(0, tree.root));
}
}
(2) BFS 풀이법
<코드>
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
class Node {
int data;
Node lt, rt;
public Node(int val)
{
data = val;
lt=rt=null;
}
}
public class Main {
Node root;
public int BFS(Node root)
{
Queue<Node> Q = new LinkedList<>();
Q.offer(root);
int L=0;
while(!Q.isEmpty())
{
int len = Q.size();
for(int i=0; i<len; i++)
{
Node cur = Q.poll();
if(cur.lt == null && cur.rt == null)
return L;
if(cur.lt != null)
Q.offer(cur.lt);
if(cur.rt != null)
Q.offer(cur.rt);
}
L++;
}
return 0;
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
// 0단계에 100번지를 넘긴다.
System.out.println(tree.BFS(tree.root));
}
}
7. 그래프와 인접행렬
- 기본 개념
G(V, E) - 그래프 G(V,E)는 어떤 자료나 개념을 표현하는 정점(vertex)들의 집합 V와 이들을 연결하는 간선(edge)들의 집합 E로 구성된 자료구조를 말한다.
인접행렬의 경우, 2차원 배열로 이를 표현한다. 아래 그림을 참고하자.
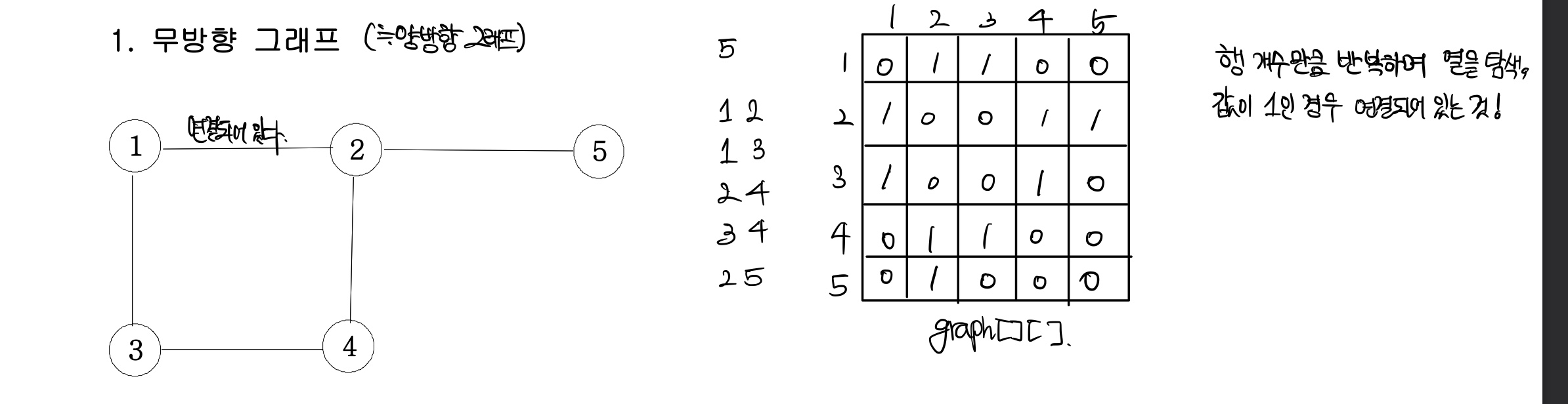
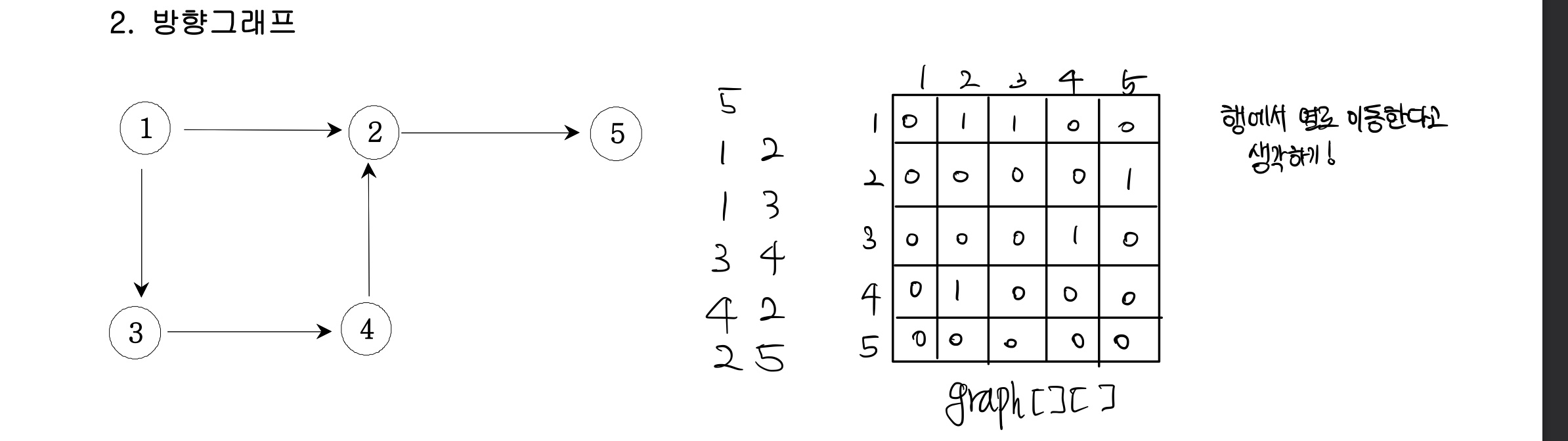

- 문제 (1. 인접행렬로 풀어보기)
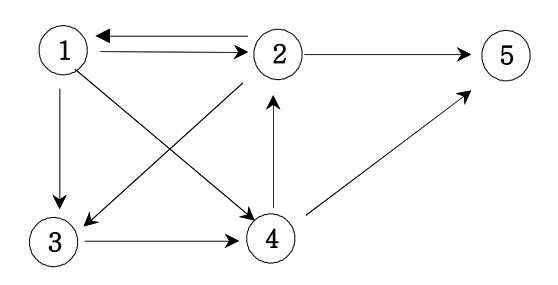
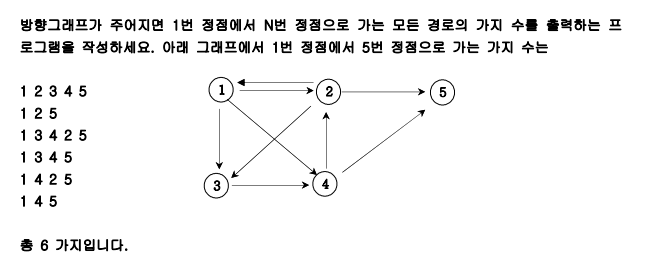
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요.
아래 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는 총 6가지이다.
| 1 2 3 4 5 1 2 5 1 3 4 2 5 1 3 4 5 1 4 2 5 1 4 5 |
 |
▣ 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연
결정보가 주어진다.
▣ 출력설명
총 가지수를 출력한다.
▣ 입력예제 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
▣ 출력예제 1
6
<코드>
import java.util.*;
public class Main {
static int n, m, answer=0;
static int[][] graph;
static int[] ch;
public void DFS(int v)
{
//처음 넘어오는 출발점 v는 1이다.
if (v==n)
answer++;
else {
for (int i = 1; i <= n; i++)
{
if(graph[v][i]==1 && ch[i] == 0)
{
ch[i]=1;
DFS(i);
//여기서부터는 back 시점.(위의 행동 취소)
ch[i]=0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new int[n+1][n+1];
ch = new int[n+1];
for(int i=0; i<m; i++)
{
int a = sc.nextInt();
int b = sc.nextInt();
graph[a][b]=1;
}
ch[1] = 1; // 출발점
T.DFS(1);
System.out.println(answer);
}
}
- 문제 (2. 인접리스트 + ArrayList로 풀어보기)
인접리스트는 정점 개수가 많을 때 효율적으로 쓸 수 있는 방법이다.
먼저, 문제를 보도록 하자.
▣ 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연
결정보가 주어진다.
▣ 출력설명
총 가지수를 출력한다.
▣ 입력예제 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
▣ 출력예제 1
6
<설명>
예를 들어, 정점이 5개라면 ArrayList 객체를 5개를 만든다. 이후 방향에 맞게 객체에 요소들을 추가해주면 된다.
* 1 -> 2 -> 3 -> 4
* 2 -> 1 -> 3
* 3 -> 4
* 4 -> 2 -> 5
* 5
이를 위해 ArrayList안에 ArrayList를 저장하도록 코드를 구현한다.
<코드>
import java.util.*;
public class Main {
static int n,m, answer=0;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch;
public void DFS(int v) {
if(v==n)
answer++;
else {
for(int nv : graph.get(v)) // v번째 ArrayList를 돈다.
{
if(ch[nv] ==0) // 방문 안했다면
{
ch[nv]=1;
DFS(nv);
ch[nv]=0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new ArrayList<ArrayList<Integer>>();
//Integer ArrayList 객체를 생성해주어야 한다.
for(int i=0; i<=n; i++)
graph.add(new ArrayList<Integer>());
ch = new int[n+1];
for(int i=0; i<m; i++)
{
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b); // index로 접근할 때 get()함수 사용.
}
ch[1]=1;
T.DFS(1);
System.out.println(answer);
}
}
8. 그래프 최단거리(BFS)

▣ 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연
결정보가 주어진다.
▣ 출력설명
1번 정점에서 각 정점으로 가는 최소 간선수를 2번 정점부터 차례대로 출력하세요.
▣ 입력예제 1
6 9
1 3
1 4
2 1
2 5
3 4
4 5
4 6
6 2
6 5
▣ 출력예제 1
2 : 3
3 : 1
4 : 1
5 : 2
6 : 2
<코드>
dis에는 각 정점에 도달할 수 있는 최소 거리를 저장한다.
즉, dis[v]라면 v까지 가는데 필요한 최소 거리를 의미한다.
import java.util.*;
public class Main {
static int n,m;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch, dis;
public void BFS(int v) {
Queue<Integer> queue = new LinkedList<>();
ch[v] = 1; // 출발 시 정점은 1
dis[v] = 0; // 출발 시 최소 거리는 0
queue.offer(v); // 1번 정점 들어간다.
while(!queue.isEmpty()) // 큐가 비어있지 않다면 ..
{
int cv = queue.poll(); // 처음 cv 값은 1일 것이다.
for(int nv : graph.get(cv))
{
if (ch[nv]==0) // 방문하지 않았을 때
{
ch[nv]=1;
queue.offer(nv);
//이 아래 줄이 제일 중요!
dis[nv]=dis[cv]+1;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
graph = new ArrayList<ArrayList<Integer>>();
//Integer ArrayList 객체를 생성해주어야 한다. (인접리스트)
for(int i=0; i<=n; i++)
graph.add(new ArrayList<Integer>());
ch = new int[n+1];
dis = new int[n+1];
for(int i=0; i<m; i++)
{
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b); // index로 접근할 때 get()함수 사용.
}
T.BFS(1); // 넓이 우선 탐색 1번부터 실행해라.
for(int i=2; i<=n; i++)
System.out.println(i+" : "+dis[i]);
}
}
'JAVA (개념, 알고리즘)' 카테고리의 다른 글
| DFS, BFS 활용 (2) (0) | 2023.02.09 |
|---|---|
| DFS, BFS 활용 (1) (0) | 2023.02.07 |
| Sorting and Searching(정렬, 이분검색과 결정알고리즘) (0) | 2023.01.29 |
| HashMap (+후반에 TreeSet에 대한 간단한 개념) (0) | 2023.01.25 |
| Two pointers, Sliding window[효율성 : O(n^2)-->O(n)] (0) | 2023.01.24 |
소중한 공감 감사합니다